
Hence, the forty-ninth term of the harmonic progression is the reciprocal of 25/6, which is equal to 6/25, which is equal to 0.24.Įxample 2: Compute the 100th term of HP if the 10th and 20th term of HP are 20 and 40 respectively. Therefore, the forty-ninth term of the arithmetic progression is 25/6. Therefore, the fifth term of the harmonic progression is the reciprocal of 1/2, which is equal to 2. The n th term of a harmonic progression is the reciprocal of the nth term in the corresponding arithmetic progression. Therefore, the fifth term of the arithmetic progression is 1/2. Now put the values in the formula, we have So, in order to find the 5th term of the A.P, use the formula: Here T2-T1 = T3-T2 = 1/12, so, 1/12 is the common difference. The arithmetic progression for the given H.P is A.P = ⅙, ¼, ⅓, …. G.M 2 = A.M x H.M, where A.M., G.M., H.M are in geometric progression A.M ≥ G.M ≥ H.M Solved Harmonic Progression ProblemsĮxample 1: Determine the 5th term and the 49th term of the harmonic progression 6, 4, 3,… S n = (1/d) x ln Comparison: Arithmetic Progression, Geometric Progression, and Harmonic Progression Relationship Between AP, GP, and HPįor any two numbers, if A, G, H are respectively the Arithmetic, Geometric, and Harmonic Mean, then the relationship between those three is given by the following formula. the sum of the harmonic progression, we use the following formula. Now, to calculate the sum of every single element in this progression i.e. Let's consider 1/a, 1/a + d, 1/a + 2d, 1/a + (n-1)d as a given harmonic progression. N - Number of Terms in A.P Sum of Harmonic Progression Formula

This can be mathematically represented by the following formula.
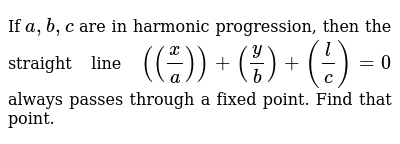
The term at the n th place of a harmonic progression is the reciprocal of the n th term in the corresponding arithmetic progression. Harmonic Mean = n / Harmonic Progressions Formula
HARMONIC PROGRESSION SERIES
The harmonic mean of a series is the reciprocal of the arithmetic mean of the reciprocal values in the series. Any term in this type of sequence is regarded as the harmonic means of its two neighbours.įor example, the series a, b, c, d, for example, is called an arithmetic progression, the harmonic progression may be written as 1/a, 1/b, 1/c, 1/d.

Building on this definition, a Harmonic Progression (HP) can be defined as a series of real numbers which is calculated by taking reciprocals of the arithmetic progression reciprocals which do not contain 0. In Mathematical terms, a progression is basically a number series which follows a specific pattern.


 0 kommentar(er)
0 kommentar(er)
