
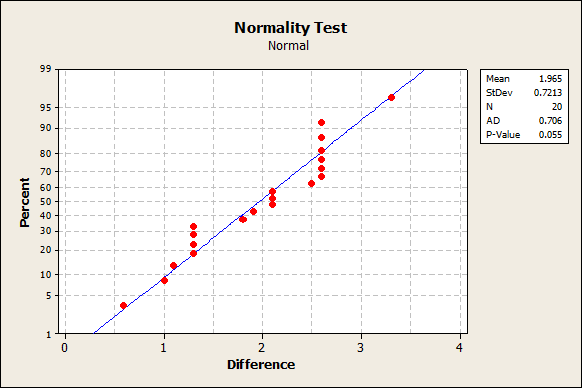
Xpu<-xp_hat + qnorm(0.975)*sqrt(v_xp_hat) #upper boundĭf.bound To add the confidence bounds as in Minitab, you can do the following fd<-fitdistr(x, "normal") #Maximum-likelihood Fitting of Univariate Dist from MASS Ggplot(data = df, aes(x = x, y = y)) + geom_point() + geom_abline(intercept = int,slope = slope)+scale_y_continuous(limits=range(qprobs), breaks=qprobs, labels = 100*probs)+labs(y ="Percent", x="Data") The following shows the line in the right spot: df It seems that geom_smooth() would be the likely candidate to add the bands, but I haven't figure that out.įinally, the Getting Genetics Done guys describe something similar here. Similarly, ggplot's stat_qq() seems to present similar information with a transformed x axis. Unfortunately, I cannot figure out how to add the confidence interval bands around this plot. The probplot gets you most of the way there. Minitab describes this as a normal probability plot. Or if your probability plot is not close to illustrate line, then you don't want to use a normal model.I am trying to recreate the following plot with R. So when you look at this and you look at the values the dots on the plot, as long as the dots are close to a straight line, then it would be a good idea to use a normal model if your history RAM is not symmetric, or if you have a long whisker, that implies outliers. And then finally the normal probability plot. But if your box plot is fairly symmetric, so if each of these regions seems to be pretty, even then a normal model would be good. So if you have a whisker that tends to be a lot longer than your box, technically, if you have a whisker that is 1.5 times the length of your inter quartile range, then you most likely have an outlier. If you're hissed, a gram is symmetric and bell shaped, not skewed, then it's probably a good idea to use the normal model for box plots. Then you need to look at your history graham. Look at your sample set, you have 100 values and that's good Because if N is greater than or equal to 30, then the central limit theorem can apply. So in determining whether or not a normal model is going to be a good distribution.

Probability plot minitab how to#



 0 kommentar(er)
0 kommentar(er)
